The Real Problem with “The Cold Equations”

Note: this a companion essay to Episode 11 of A Reader’s History of Science Fiction.

“The Cold Equations” is a 1954 short story written by Tom Godwin and published in Astounding Science Fiction under its longtime editor, John W. Campbell. This story is a unique work of art. It may well be the most famous-in-its-own-right short story in the history of science fiction—by which I mean it wasn’t written by a famous author like “The Last Question” by Isaac Asimov, and it’s not known for its adaptations like “Story of Your Life” by Ted Chiang (which was adapted into the movie Arrival), or for being part of a franchise like Star Trek. Tom Godwin was a true one hit wonder of science fiction. None of his other stories or novels have become a fraction as well-known. Instead, “The Cold Equations” was catapulted to fame solely on the basis of its shocking and deliberately disturbing plot.

As popular as this story is, it has also been enormously controversial. Many people have criticized it for many reasons. There are social criticisms like the sexism pervading the story or the fact that it seemed to be plagiarized from the comic book Weird Science—both probably true given Campbell’s personality (although Weird Science itself was a shameless plagiarist). But the biggest criticism has always been the incredible levels in-story human error and downright absurd engineering. However, I go a step further.

I think Godwin and Campbell got the equations themselves wrong.

---

“The Cold Equations” takes place on a spaceship that is delivering emergency medical supplies to Woden, a distant colony world. The ship is stripped down as much as physically possible to get there fast and cheap. The pilot, Barton, discovers he has a stowaway on board, an eighteen-year-old girl named Marilyn, who snuck on board in hopes of visiting her brother at the colony. But her presence on the ship is a deadly problem: the ship doesn’t have enough fuel.

Barton’s ship was dispatched from a mothership (so there’s no messy launch from a planet to worry about) and has the bare minimum that it needs to reach its destination. The ship can travel through hyperspace from one star to another for free, but once it arrives, it’s still going the same speed as the mothership, while Woden isn’t. It needs to burn fuel to account for the relative motion between the ship and the planet. This change in velocity, or delta-v, is a hard limit on what the ship must do to arrive safely. And a small amount of fuel can make a big difference. Basically, you need more fuel to lift the fuel, so as your delta-v increases, the fuel requirements go up exponentially. With Marilyn’s added weight, the incredibly finely-balanced ship won’t have enough fuel to land.

Regulations say that stowaways are to be shot on sight and jettisoned out the airlock for this very reason. They have to get rid of the extra weight. Barton, being human, doesn’t want to do this, but if he doesn’t, the ship will crash, and Marilyn will die anyway, plus himself and multiple people on the ground. The “cold equations” of physics admit no other solution, and in the end, Marilyn willingly lets herself be jettisoned into space.

---

It’s a shocking ending, and in fact, it wasn’t even Godwin’s idea. It was Campbell’s. As the editor, he had the final say over publication, and he made Godwin rewrite the story three times because, according to writer Joseph Green, “Godwin kept coming up with ingenious ways to save the girl!” Because in any reasonable situation, that would have been easily doable, but Campbell thought it would make a better story if she died.

Like many, many physicists, engineers, and sci-fi authors, this story has never sat well with me—and that’s kind of the point. The story was a deliberate subversion of the more standard stories that were common at the time where the hero pulls off some clever trick to save the girl. It’s supposed to be uncomfortable. But even so, when he wrote it, we can see that Godwin had a hard time himself coming up with a scenario that really did have no solution.

People have since pointed out that there were multiple non-ridiculous solutions available, but these can all be explained away as flaws in the composition of the story. No, the feeling I had that something wasn’t quite right about the story went deeper than that—something I couldn’t articulate beyond an unsubstantiated instinct that the equations themselves weren’t as cold as Godwin said.

But I finally looked in the right place, and I think I found the real reason this story is wrong.

It’s not the absolute lack of a safety margin for fuel, where even a one percent error will cause the ship to crash. It’s an emergency ship, after all…even though that’s a ridiculously tiny margin even for an emergency ship. Typical safety margins for spacecraft are at least 30%, and anything less than 5% is a rounding error. (Here’s a NASA study to that effect.) But those are engineering tolerances, not fuel capacity. Fuel is a little weirder, as I explain below, so I’ll give him that one.

It’s not the breathtaking lack of security. Sure, there was a complete lack of a simple preflight check. (Just double-checking that the cargo was on board would have found Marilyn out.) And the ship probably could have detected the weight discrepancy at launch if it had any kind of decent equipment. And yes, there was no lock on the entrance, and the warning sign only said, “UNAUTHORIZED PERSONNEL KEEP OUT!” instead of “STOWAWAYS WILL BE SHOT! NO EXCEPTIONS!” But I’ll let it all slide. As James Cameron says, the script says Jack had to die, so any human error that’s necessary for that to happen will happen.

It’s not that the ship supposedly has zero safety margin when there are probably other ways to shed the excess weight. Godwin does a good job of closing off most of the options. There’s nothing else in the supply closet but the medicine. There’s no mention of any other supplies or equipment on board. There’s not even any mention of spacesuits, even though a real spaceship wouldn’t be caught dead without one even if they had to throw everything else out, doubly so if it was running on such thin margins.

Even so, the options are not zero. Depending how the ship is set up, it might be possible to remove the pilot’s chair and the door to the supply closet and jettison those instead. Don Saker’s rebuttal to the story, “The Cold Solution” has the (now-female) pilot cutting her own legs off to make up the difference in weight. But before they resort to that, air has mass, and the ship seems to be big enough that they might be able to vent enough of the air to lighten the ship while still leaving them enough to carry out the landing. But no, all that can be chalked up to sloppy writing. It doesn’t automatically invalidate the premise.

It’s not that being able to change trajectories to buy an hour, as they do in the story, implies there really is a safety margin. Actually, there was probably a margin in the trajectory all along. It’s just that it was balancing fuel against time. It’s very often possible to change trajectories in space in a way that will save fuel—which is kind of important because by the time Marylin is discovered, the ship has already lost some of its margin.

In fact, there are often low-energy trajectories that will reduce the fuel requirements a lot—for some paths, to almost zero! But they can take weeks or even months. Now, the problem is that the ship’s life support won’t last long enough. It’s entirely possible that the extra hour was a lucky break, and anything that used less fuel than that would require spending days looping around a moon or something. None of these things get at the root of the problem.

The real problem with this story is that the rocket equation does not work that way!

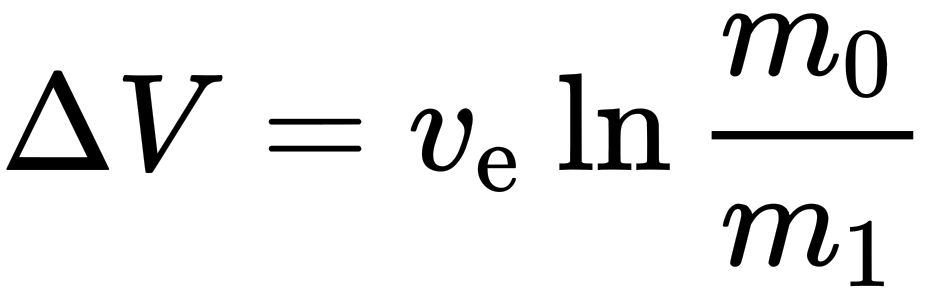
This is the rocket equation, discovered by Russian physicist Konstantin Tsiolkovsky in 1903. (Although British mathematician William Moore also figured it out a century earlier.) It says that the change in velocity, or delta-v, that a rocket is able to make is proportional to its exhaust velocity (an intrinsic property of the fuel and the design of the engines) and the logarithm of the ratio of “takeoff” mass (m₀) to “dry” or “final” mass (m₁)—in other words, how much more the rocket weighs with fuel than without.

If you turn the rocket equation around, you get this.

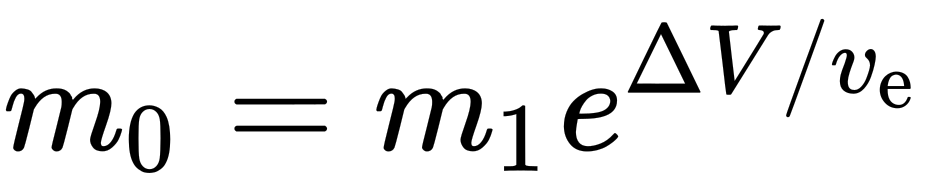
This is the equation that ends so tragically for Marilyn. This is an exponential function. They can be a little hard to read if you’re not familiar with them, but it simple terms, it means that for every little bit faster you want to go (usually in the ballpark of 3 km/s or 7,000 miles per hour), you have to double the amount of fuel you’re carrying. Again, you need more fuel to lift the fuel, and so on, so even if you only need to go a little bit faster (by rocket standards), you need a lot more fuel.

But here’s the problem: in the rocket equation, fuel requirements increase exponentially with speed, but only linearly with weight. A six-ton ship needs only 20% more fuel than a five-ton ship. And if Barton’s ship weighs five tons empty (and this is less than the Apollo capsules, which were very likely smaller), Marylin would add about one percent to its mass, and a one percent increase in dry mass equals a one percent shortfall in fuel mass. Basically, you’re replacing m₁ in that equation with 1.01m₁.

How much delta-v would the ship lose from that one percent shortfall in fuel? If you do the math, it turns out to be one percent of the fuel’s exhaust velocity. For typical rocket engines, that comes out to about 100 miles per hour (160 km/h)—and here’s the weird part: regardless of the total amount of fuel.

That’s hard for me to wrap my brain around, but I think it’s simply that, just as you need more fuel to lift the fuel, when you burn more fuel than you expected, there’s less that you have to move later, and it balances out. No matter how much fuel Barton’s ship carries, they’re always going to reach the planet going about 100 miles per hour too fast.

Now, here’s where the obvious solution comes in. The ship is going to run out of fuel and won’t be able to land? Maybe just turn the engines off, and save some fuel for the landing. The ship will hit the atmosphere going 100 miles per hour too fast, but that’s not a problem because there’s one part of the ship that absolutely must have more than a one percent safety margin: the heat shield! That’s because the properties of Earth’s upper atmosphere can easily vary by 10% based on things like solar activity and weather. The equations are never going to be precise to the last gram there, so the ship needs to be built to handle a rougher reentry. Problem solved.

So, there are two possible responses to this. First is that Godwin wrote the story in 1954, before we had sent anything into orbit, so we didn’t really understand how reentry worked yet, and he might not have known that solution. Although even then, some other option like a water landing or even a different landing site (given the rotation of the planet) might be possible.

Second, since Godwin (or rather Campbell) was trying to close off all solutions, what if the ship was not going to a planet, but to a space station? Then, there would be no atmosphere to slow it down, and yes, the equations would work the way he wanted…but really? Would a space station really not have some kind of shuttle that could make the 200 mile-per-hour round trip to go and intercept the ship and bring it in? The fuel requirement would be a pittance—five hundred pounds (230 kg) with a generous safety margin, only a few percent the mass of the ship. So, yes, you could technically make it work, but the story would have to be twice as contrived as it already is. The equations were wrong.

Now, after all this, I don’t want to tear this story apart without suggesting an alternative, and as an alternative, I would recommend reading the novel Gateway by Frederick Pohl. I don’t want to spoil it, but it addresses similar themes to “The Cold Equations” and actually delves deeper into the consequences of those themes while being far less contrived than Godwin’s story.